
알고리즘의 성능과 평가
만약 우리가 집에서 여행을 떠나기 위해 출발하여 목적지까지 가는 방법에 대한 알고리즘을 생각해본다면 여러 방법이 있을 겁니다. 걸어서 가는 방법, 자전거를 타고 가는 방법, 대중교통을 타고 가는 방법 그리고 중간에 카페에 들러 커피를 사거나 서점에 들러 책을 읽다가 갈 수도 있습니다. 이렇게 무수히 많은 경우에 수가 있지만 어떤 방법이 가장 빠르고 효율적인지 판단하기 어렵습니다.
위 제시했던 모든 방법들이 여행지에 도착이라는 목적을 달성하지만 가장 빠르고 효율적으로 도착하지는 않습니다. 알고리즘도 주어진 문제를 해결하기 위해 어떤 알고리즘을 선택해서 해결할지 결정해야 합니다. 시간적 측면과 공간적 측면을 비교하여 어떤 알고리즘을 활용할지 선택을 도울 수 있는 방법을 알아보겠습니다.
복잡도, Complexity
문제 해결을 위해 적절한 알고리즘을 결정하기 위해서 각각의 성능을 평가해봐야 합니다. 이때 평가를 위해 '복잡도'를 척도로 사용합니다. 복잡도는 시간 복잡도와 공간 복잡도의 개념이 있으며 동일한 기능을 수행하는 알고리즘의 경우 복잡도가 낮을수록 효율적인 알고리즘이라고 판단합니다.
공간 복잡도
공간 복잡도란 데이터 관리에 필요한 공간을 나타내는 개념입니다. 알고리즘 과정에서 얼마나 많은 공간(메모리)을 차지하는지 분석하는 것입니다. 데이터의 흐름에 따라 공간이 어떻게 변하는지 표현하고 측정할 수 있게 도와주는 지표입니다. 간단히 특징을 알아보겠습니다.
- 시간과 공간은 반비례적인 경향이 있음
- 배열의 크기, 동적 할당 여부, 재귀 함수 등이 영향을 줌
- 고정 공간과 가변 공간, 가변 공간을 사용할 수 있는 구조가 더 효율적
요즘은 공간 복잡도 보다 시간 복잡도를 훨씬 중요하게 다룹니다. 그 이유는 하드웨어 성능이 과거에 비해 크게 발전해서 공간이 넘쳐나다 보니 개발 과정에서 메모리 문제에 대해 과거처럼 신경 쓰지 않습니다. 하지만 시간 복잡도의 경우 잘못 구성하게 되면 프로그램이 너무 느려지기 때문에 사용자 입장에서 불편을 느끼게 됩니다.
시간 복잡도
시간 복잡도란 알고리즘이 데이터를 처리하는 데 걸리는 시간을 나타내는 개념입니다. 많은 개발자들이 시간 복잡도를 통해 프로그램의 실행 시간을 줄이기 위해 많은 노력을 합니다. 점근 표기법으로 공간 복잡도와 시간 복잡도를 표현하는데 위에 설명했던 것처럼 시간 복잡도를 훨씬 중요하게 다루기 때문에 점근 표기법으로 주로 시간 복잡도를 표현하는 데 사용합니다. 복잡도를 표현하는 점근 표기법, 그중에서도 빅오 표기법에 대해서 자세히 알아보겠습니다.
시간 복잡도는 실행 시간의 효율성, 공간 복잡도는 메모리의 효율성
점근 표기법
점근 표기법이란 알고리즘의 성능을 수학적으로 표현하는 방법입니다. 즉 알고리즘의 효율성을 평가하는 수학적 도구이며 최선의 경우, 평균적인 경우, 최악의 경우를 표현합니다. 가장 큰 영향력이 있는 항만 표시한다는 점과 상수항은 무시한다는 특징이 있습니다.
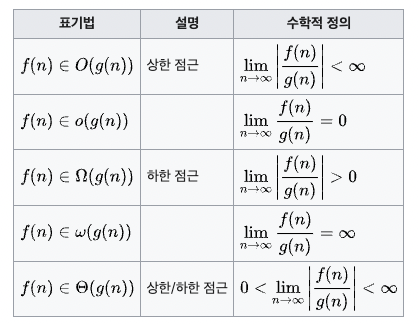
- 빅 오 표기법, Big O: O - 최악의 경우, Worst Case - 상한 점근
- 빅 오메가 표기법, Big Omega: Ω - 최선의 경우, Best Case - 하한 점근
- 빅 세타 표기법, Big Theta: Θ - 평균적인 경우, Average Case - 상한/하한 점근
빅 오 표기법, Big-O Notation
프로그램은 대부분 입력값이 최선의 경우일 가능성이 적을뿐더러 항상 최악의 경우를 대비해야 하기 때문에 시간 복잡도를 확인할 때 빅 오 표기법을 사용합니다. 현업에서 복잡도에 대한 얘기를 나눈다면 항상 빅오 표기법을 기준으로 얘기한다고 생각해도 괜찮습니다.
알고리즘의 성능 평가는 시간 복잡도만, 그중에서도 빅오 표기법을 기준
빅 오(Big-O)의 특징
빅 오 표기법의 특징은 시간 복잡도에 미미한 영향을 주는 값들은 무시하는 점입니다. 첫 번째로 상수항을 무시합니다. 어떤 알고리즘이 O(N+3)의 복잡도를 가졌다면 상수를 생략하고 O(N)으로 표기합니다. 두 번째로 입력 크기가 클 때 계수도 무시합니다. 알고리즘의 복잡도가 O(2N)의 복잡도를 가졌다면 계수를 생략하고 O(N)으로 표기합니다. 세 번째로 가장 큰 영향력이 있는 항, 즉 최고차 항만 표기합니다. 알고리즘이 O(N²+4N+2)의 복잡도를 가졌다면 O(N²)으로만 표기합니다.
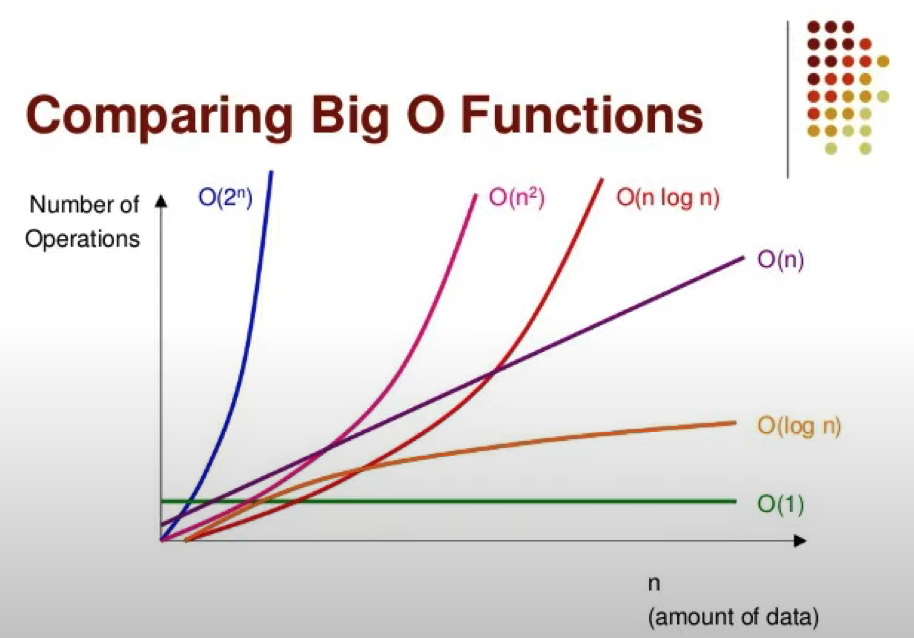
O(1) < O(㏒ N) < O(N) < O(N ㏒ N) < O(N²) < O(2ⁿ)
상수 함수 < 로그 함수 < 선형 함수 < 다항 함수 < 지수 함수
오른쪽으로 갈수록 효율이 떨어진다.
빅 오(Big-O)의 종류와 예제
1. O(1), 상수
입력 데이터의 크기에 상관없이 언제나 일정한 시간이 걸리고 데이터의 양이 증가해도 성능에 거의 영향을 미치지 않습니다. 예제는 Stack의 Push, Pop이 대표적입니다.
2. O(㏒ N), 로그
입력 데이터의 크기가 커질수록 처리 시간이 로그만큼 짧아집니다. 예를 들어 데이터가 10배가 되면 처리 시간은 2배가 됩니다. 예제는 이진트리가 대표적이며 재귀가 순기능으로 이루어지는 경우에도 해당됩니다.
3. O(N), 선형
입력 데이터의 크기에 비례해 처리 시간이 증가합니다. 예를 들어 데이터가 10배가 되면 처리 시간도 10배가 됩니다. 예제는 for 문이 대표적입니다.
4. O(N ㏒ N), 선형 로그
입력 데이터가 많아질수록 처리 시간이 로그 배만큼 더 늘어납니다. 예를 들어 데이터가 10배가 되면 처리 시간은 약 20배가 됩니다. 예제는 퀵 정렬(Quick Sort), 합병 정렬(Merge Sort), 힙 정렬(Heap Sort)이 대표적입니다.
5. O(N²), 다항
입력 데이터가 많아질수록 처리시간이 급수적으로 늘어납니다. 예를 들어 데이터가 10배가 되면 처리 시간은 최대 100배가 됩니다. 예제는 삽입 정렬(Insertion Sort), 버블 정렬(Bubble Sort), 선택 정렬(Selection Sort), 이중 for 문이 대표적입니다.
6. O(2ⁿ), 지수
입력 데이터가 많아질수록 처리시간이 기하급수적으로 늘어납니다. 예제는 피보나치(Fibonacci) 수열이 대표적이며 재귀가 역기능으로 이루어질 경우에도 해당됩니다.
정렬 알고리즘 특징/종류/시간 복잡도 [ 선택, 삽입, 버블, 합병, 힙, 퀵, 기수 ]
알고리즘이 무엇인가? 알고리즘은 어떤 문제를 해결하기 위한 동작들의 절차입니다. 일상에서 보면 내가 목적지까지 가기 위한 과정을 말하기도 하고 프로그래밍에서는 입력받은 인풋을 통해
aiday.tistory.com
참고하면 좋은 영상
내용 참고
한양대학교 인공지능융합대학원 컴퓨터 알고리즘 강의자료, 미남님 블로그, 코딩 캠프님 블로그
'ALGORITHM > Concept' 카테고리의 다른 글
| [알고리즘] 누적합, Prefix Sum (feat. Python, Javascript) (88) | 2023.04.14 |
|---|---|
| [알고리즘] 완전 탐색, 브루트 포스 정의 | 종류 | 장단점 | 예시 (feat. Node.js Brute-Force-Search) (32) | 2023.03.17 |
| 정렬 알고리즘 특징/종류/시간 복잡도 [ 선택, 삽입, 버블, 합병, 힙, 퀵, 기수 ] (80) | 2022.10.27 |
